
We know how to calculate this for a body undergoing translational motion, but how about for a rigid body undergoing rotation? This might seem complicated because each point on the rigid body has a different velocity. Rotational Kinetic EnergyĪny moving object has kinetic energy.
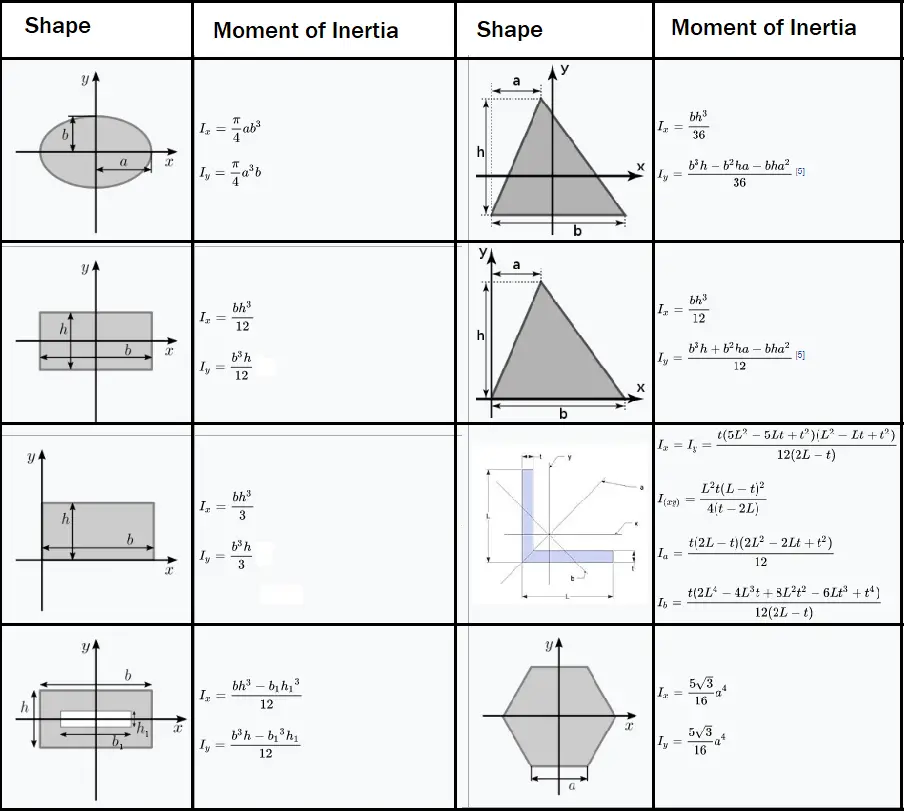
With these properties defined, we will have two important tools we need for analyzing rotational dynamics. In this section, we define two new quantities that are helpful for analyzing properties of rotating objects: moment of inertia and rotational kinetic energy. So far in this chapter, we have been working with rotational kinematics: the description of motion for a rotating rigid body with a fixed axis of rotation. Calculate the angular velocity of a rotating system when there are energy losses due to nonconservative forces.Use conservation of mechanical energy to analyze systems undergoing both rotation and translation.Explain how the moment of inertia of rigid bodies affects their rotational kinetic energy.
Define the physical concept of moment of inertia in terms of the mass distribution from the rotational axis.Describe the differences between rotational and translational kinetic energy.By the end of this section, you will be able to:


 0 kommentar(er)
0 kommentar(er)
